Our puny scientist minds can’t grasp pizza deals (Guest & Martin 2021; postscript to data-driven science)

In the last post about conceptions of data-driven science, I wrote about the idea that reality is so complicated that we might need computers to help us reason about it. To be fair, even simple relationships in small data are too much for our puny brains to handle intuitively. We need to do the calculations. Here is Guest & Martin’s Pizza Problem of scientific reasoning, as presented in a thread by @cretiredroy on Twitter:

I ordered a 9-inch Pizza.
After a while, the waiter brought two 5-inch pizzas and said, the 9-inch pizza was not available and he was giving me two 5-inches Pizzas instead, and that I am getting 1 inch more for free!

The area of a circle is pi times the square of the radius r. A number n of 5-inch pizzas is smaller than a 9-inch pizza if:

Which we can rearrange to:

@cretiredroy again:

I said that even if he gave three pizzas, I would still lose-out.
”How can you say you are giving me an extra inch for free?”
The owner was speechless.
He finally gave me 4 pizzas.

Take Maths seriously!

Guest & Martin (2021) use this simple problem as their illustration for computational model building: two 5 inch pizzas for the same price as one 9 inch pizza is not a good deal, because the 9 inch pizza contains more food. As I said before, I don’t think in inches and Swedish pizzas usually come in only one size, but this is counterintuitive to many people who have intuitions about inches and pizzas.

(In Guest & Martin's paper, the numbers are actually 12 and 18 inches. We can generalise to any radiuses of big and small pizzas:

Plugging in 12 and 18 gives 2.25, meaning that three 12-inch pizzas would be needed to sweeten the deal.)

We assume that we already agree that the relevant quantity is the area of pizza that we get. If we were out to optimise the amount of crust maybe the circumference, which is 2 times pi times the radius r, would be more relevant. In that case:

And the two smaller pizzas are a better deal with respect to crust circumference.

The risk of inconsistencies in our scientific understanding because we cannot intuitively grasp the implications of our models is what Guest & Martin call "The pizza problem". They believe that it can be ameliorated by computational modelling. If we have to make the calculations, we will notice and have to deal with assumptions we would otherwise not think about.

This is a different benefit of doing the calculations than the intuition building I wrote about in my post about the Monty Hall problem:

The outcome of the simulation is less important than the feeling that came over me as I was running it, though. As I was taking on the role of the host and preparing to take away one of the losing options, it started feeling self-evident that the important thing is whether the first choice is right. If the first choice is right, holding is the right strategy. If the first choice is wrong, switching is the right option. And the first choice, clearly, is only right 1/3 of the time.

I don’t think anyone is saying that it is impossible to intuitively grasp the case of the pizza deals. If you are used to relationships with squares, you might do it as quickly as @cretiredroy in the Twitter thread. However, because even simple power law relationships and probability experiments are tricky for us to reason about when we are naive to them, that should give us pause about our ability to reason verbally about new causal patterns. We might need some help.

Guest & Martin use the pizza example to illustrate their model of science as a hierarchy of frameworks, theories, specifications, implementations, hypotheses and data. The "framework" contains concepts of pizza, food and order, leading to the idea to maximize the amount of food per order. Our decision to care about amount of pizza and not about crust circumference belongs here. They describe two competing "theories": one that we need to maximise surface area and one that we need to maximise number of pizzas. The specification is the model of the area of a circle, and the implementation is plugging the numbers into it.

They argue that the "theory", "specification" and "implementation" steps are often omitted, and that doing so (prematurely jumping on to data collection), leads to inconsistencies that could have been avoided by being explicit about these steps. That is, in the pizza case, one should first write down the equations for the surface area of pizzas and compute the results before ordering the two deals and weighing the pizzas.

Just writing down the equations is not enough. In their talk on the topic for Glasgow ReproducibiliTea, Guest & Martin (2020) emphasise that the pizza problem is an issue even when we already have a formal model that describes the problem well — as in the pizza case, everyone agrees on the maths of the area of a circle — but that does not prevent the result from being counterintuitive. The formal model does not actually help resolve the confusion until it is used to compute the area of the two pizza orders.

I wanted to illustrate this post with a photo of a pizza from the chippy in Penicuik, where you get a complimentary box of chips with the larger size pizza, but I couldn’t find it. Instead, here are some pizzas from #GeneticistsTweetingAboutPizza.

References

@cretiredroy Twitter thread https://twitter.com/cretiredroy/status/1542351846903529472

Guest, O., & Martin, A. E. (2021). How computational modeling can force theory building in psychological science. Perspectives on Psychological Science, 16(4), 789-802.

Guest O & Martin (2020). How computational modeling can force theory building in psychological science (Glasgow ReproTea). Recording. https://www.youtube.com/watch?v=_WV7EFvFAB8

Levels of data-driven science

This list of gradually more radical conceptions represent my attempt at understanding the term ”data-driven science”. What does it mean?

Level 0: ”All science is already data-driven”

This is the non-answer that I expect from researchers who take ”data-driven” to mean ”empirical science as usual”, potentially distinguishing it from ”theory”, which they may dislike.

Level 1: ”My science is already data-driven”

This is the answer I expect from the ”milk recordings are Big Data” crew, i.e., researchers who are used to using large datasets, and don’t see anything truly new in the ”Big Data” movement (but might like to take part in the hype with their own research).

For example, Leonelli (2014) writes about developments in model organism databases and their relation to ”Big Data”. She argues that working with large datasets was nothing new for this community but that the Big Data discourse brought attention to the importance of data and data management:

There is strong continuity with practices of large data collection and assemblage conducted since the early modern period; and the core methods and epistemic problems of biological research, including exploratory experimentation, sampling and the search for causal mechanisms, remain crucial parts of inquiry in this area of science – particularly given the challenges encountered in developing and applying curatorial standards for data other than the high-throughput results of ‘omics’ approaches. Nevertheless, the novel recognition of the relevance of data as a research output, and the use of technologies that greatly facilitate their dissemination and re-use, provide an opportunity for all areas in biology to reinvent the exchange of scientific results and create new forms of inference and collaboration.

Level 2: Re-using data as much as possible

This answer is the notion that data-driven research is about making use of the data that is already out there as much as possible, putting it in new research contexts and possibly aggregating data from many sources.

This is the emphasis of the SciLife & Wallenberg program for ”data-driven life science”:

Experiments generate data, which can be analyzed to address specific hypotheses. The data can also be used and combined with other data, into larger and more complex sets of information, and generate new discoveries and new scientific models. Which, in their turn, can be addressed with new experiments.

Researchers in life science often collect large amounts of data to answer their research questions. Often, the same data can be used to answer other research questions, posed by other research groups. Perhaps many, many other questions, and many, many other research groups. This means that data analysis, data management and data sharing is central to each step of the research process …

In my opinion, taking this stance does not necessarily imply any ban on modelling, hypothesising or theorising (which is the next level). It’s a methodological emphasis on data, not a commitment to a particular philosophy of science.

Level 3: A philosophy of science that prioritises data exploration

This answer understands ”data-driven science” as a philosophy of science position that prioritises data exploration over modelling, hypothesising and theorising. Leonelli argues that this is one of the key features of data driven research (2012).

Extreme examples include Chris Anderson’s view that ”correlation is enough” and that large datasets have made theories and searches for causes obsolete. Anderson wrote in Wire 2008 about how ”petabyte-scale” data is making theory, hypotheses, models, and the search for causes obsolete.

The new availability of huge amounts of data, along with the statistical tools to crunch these numbers, offers a whole new way of understanding the world. Correlation supersedes causation, and science can advance even without coherent models, unified theories, or really any mechanistic explanation at all.

But faced with massive data, this approach to science — hypothesize, model, test — is becoming obsolete. Consider physics: Newtonian models were crude approximations of the truth (wrong at the atomic level, but still useful). A hundred years ago, statistically based quantum mechanics offered a better picture — but quantum mechanics is yet another model, and as such it, too, is flawed, no doubt a caricature of a more complex underlying reality. The reason physics has drifted into theoretical speculation about n-dimensional grand unified models over the past few decades (the ”beautiful story” phase of a discipline starved of data) is that we don’t know how to run the experiments that would falsify the hypotheses — the energies are too high, the accelerators too expensive, and so on.

/…/

There is now a better way. Petabytes allow us to say: ”Correlation is enough.” We can stop looking for models. We can analyze the data without hypotheses about what it might show. We can throw the numbers into the biggest computing clusters the world has ever seen and let statistical algorithms find patterns where science cannot.

I believe that this extreme position is incoherent. We can’t infer directly from data without a theory or model. The options are to do it with or without acknowledging and analysing the models we use. But there are less extreme versions that make more sense.

For example, van Helden (2013) argued that omic studies imply more broad and generic hypotheses, about what kinds of mechanisms and patterns one might expect to find in a large dataset, rather than hypothesising the identity of the genes, pathways or risk factors themselves.

Equipped with such huge data sets, we can perform data mining in an objective way. For some purists, this approach to data acquisition is anathema, as it is not ‘hypothesis-driven’. However, I submit that it is. In this case, the original hypothesis is broad or generic–we generate data, assess it and probably find something useful for elucidating our research problem. /…/ The hypothesis is that one will design an algorithm and find a pattern, which allows us to distinguish between cases and controls.

Anderson might be right that the world as revealed by data is too complicated for our puny brains to write down equations about; maybe machines can help. That brings us to the next level.

Level 4: Machine learning to replace scientific reasoning

This answer is the attitude that complex relationships in large data are too much for the human mind, and traditional theoretical models, to handle. Instead, we should use machine learning models to find patterns and make predictions using automated inference processes that are generally too intricate for humans to interpret intuitively. This is also one of Leonelli’s key features of data-driven research (2012).

Again, Anderson’s ”End of Theory” is an extreme example of this view, when he argues that the complex interactions between genes, epigenetics and environment make theoretical models of genetics useless.

Now biology is heading in the same direction. The models we were taught in school about ”dominant” and ”recessive” genes steering a strictly Mendelian process have turned out to be an even greater simplification of reality than Newton’s laws. The discovery of gene-protein interactions and other aspects of epigenetics has challenged the view of DNA as destiny and even introduced evidence that environment can influence inheritable traits, something once considered a genetic impossibility.

In short, the more we learn about biology, the further we find ourselves from a model that can explain it.

Anderson overstates how helpless genetic models are against complexity, but there is a point here, for example with regard to animal breeding. Part of what made genomics useful in modern animal breeding was giving up on the piecemeal identification of individual markers of large genetic effect, and instead throwing whole-genome information into a large statistical model. We estimate them all, without regard for their individual effect, without looking for genetic causes (”genetics without genes” as Lowe & Bruce (2019) put it), and turn them into a ranking of animals for selection decisions. However, this is level 3 stuff, because there is a human-graspable quantitative genetic theory underlying the whole machinery, with marker effect, breeding values, and equations that can be interpreted. A more radical vision of machine learning-based breeding would take away that too, no notion of genetic relationship between individuals, genetic correlation between traits, or separating genotype from phenotype. Will this work? I don’t know, but there are tendencies like this in the field, for example when researchers try to predict useful traits from high-dimensional omics or sensor data.

Apart from those pro-machine learning, anti-theory stances, you could have a pro-machine pro-theory stance. There several fields of research that try to use automated reasoning to help do theory. One interesting subfield of research that I only learned about recently is research around ”symbolic regression” and ”machine scientists” where you try to find mathematical expressions that fit data but allowing for a large variety of different expressions. It’s like a form of model selection where you allow a lot of flexibility about what kind of model you consider.

There is a whole field of this, but here is an example I read recently: Guimerà et al. (2020) used a Bayesian method, where they explore different expression with Markov Chain Monte Carlo, putting a prior on the mathematical expression based on equations from Wikipedia. This seems like something that could be part of a toolbox of a data-driven scientist who still won’t give up on the idea that we can understand what’s going on, even if we might need a help from a computer.

References

Anderson C., The End of Theory: The Data Deluge Makes the Scientific Method Obsolete. Wired.

van Helden P., 2013 Data-driven hypotheses. EMBO reports 14: 104–104.

Leonelli S., 2012 Introduction: Making sense of data-driven research in the biological and biomedical sciences. Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences 43: 1–3.

Leonelli S., 2014 What difference does quantity make? On the epistemology of Big Data in biology. Big Data & Society 1: 2053951714534395.

Lowe, James WE, and Ann Bruce., 2019 Genetics without genes? The centrality of genetic markers in livestock genetics and genomics. History and Philosophy of the Life Sciences 41.4

Guimerà, R., Reichardt, I., Aguilar-Mogas, A., Massucci, F. A., Miranda, M., Pallarès, J., & Sales-Pardo, M., 2020. A Bayesian machine scientist to aid in the solution of challenging scientific problems. Science advances, 6(5), eaav6971.

Simulating shared segments between relatives

A few months ago I saw this nice figure from Amy Williams of the number of DNA segments that are expected to be shared between relatives. I thought it would be fun to simulate segment sharing with AlphaSimR.

Because DNA comes in chromosomes that don’t break up and recombine that much, the shared DNA between relatives tends to come in long chunks — segments that are identical by descent. The distribution of segment lengths can sometimes be used to tell apart relationships that would otherwise give the same average (e.g., Yengo et al. 2019, Qiao et al. 2021).

But let’s not do anything sophisticated. Instead, we take three very simple pedigrees — anyone who’s taken introductory genetics will recognize these ones — and look at relationships between full-sibs, half-sibs and cousins. We’ll also look at the inbred offspring of matings between full-sibs, half-sibs and cousins to see that the proportion that they share between their two copies of the genome lines up with the expected inbreeding.

There won’t be any direct comparison to the values that Williams’ simulation, because it simulated more distant relationships than this, starting with cousins and then moving further away. This is probably more interesting, especially for human genealogical genetics.

The code is on GitHub if you wants to follow along.

The pedigrees

Here are the three pedigrees, drawn with the kinship2 package:

A pedigree, here, is really a table of individuals, where each column tells us their identifier, their parents, and optionally their sex, like this:

id, mother, father, sex
1, NA, NA, M
2, NA, NA, F
3, NA, NA, M
4, 2, 1, F
5, 2, 1, M
6, NA, NA, F
7, 4, 3, M
8, 6, 5, F
9, 8, 7, F

We can use GeneticsPed to check the relatedness and inbreeding if we don’t trust that I’ve entered the pedigrees right.

library(GeneticsPed)
library(purrr)
library(readr)

ped_fullsib <- read_csv("pedigrees/inbreeding_fullsib.txt")
ped_halfsib <- read_csv("pedigrees/inbreeding_halfsib.txt")
ped_cousin <- read_csv("pedigrees/inbreeding_cousin.txt")

inbreeding_ped <- function(ped) {

    inbreeding(Pedigree(ped))

}

print(map(list(ped_fullsib, ped_halfsib, ped_cousin), inbreeding_ped))

[[1]]
   1    2    3    4    5 
0.00 0.00 0.00 0.00 0.25 

[[2]]
    1     2     3     4     5     6 
0.000 0.000 0.000 0.000 0.000 0.125 

[[3]]
     1      2      3      4      5      6      7      8      9 
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0625

Comparing haplotypes

We need some functions to compare haplotypes and individuals:

library(AlphaSimR)
library(dplyr)
library(purrr)
library(tibble)

## Find shared segments between two haplotypes expressed as vectors
## map is a vector of marker positions

compare_haplotypes <- function(h1, h2, map) {
    sharing <- h1 == h2

    runs <- rle(sharing)
    end <- cumsum(runs$lengths)
    start <- c(1, end[-length(end)] + 1)

    segments <- tibble(start = start,
                       end = end,
                       start_pos = map[start],
                       end_pos = map[end],
                       segment_length = end_pos - start_pos,
                       value = runs$values)

    segments[segments$value,]
}

We will have haplotypes of the variants that go together on a chromosome, and we want to find segments that are shared between them. We do this with a logical vector that tests each variant for equality, and then use the rle to turn this into run-length encoding. We extract the start and end position of the runs and then keep only the runs of equality.

Building on that function, we want to find the shared segments on a chromosome between two individuals. That is, we make all the pairwise comparisons between the haplotypes they carry and combine them.

## Find shared segments between two individuals (expressed as
## matrices of haplotypes) for one chromosome

compare_individuals_chr <- function(ind1, ind2, map) {

    h1_1 <- as.vector(ind1[1,])
    h1_2 <- as.vector(ind1[2,])

    h2_1 <- as.vector(ind2[1,])
    h2_2 <- as.vector(ind2[2,])

    sharing1 <- compare_haplotypes(h1_1, h2_1, map)
    sharing2 <- compare_haplotypes(h1_1, h2_2, map)
    sharing3 <- compare_haplotypes(h1_2, h2_1, map)
    sharing4 <- compare_haplotypes(h1_2, h2_2, map)

    bind_rows(sharing1, sharing2, sharing3, sharing4)
}

Finally, we use that function to compare individuals along all the chromosomes.

This function takes in a population and simulation parameter object from AlphaSimR, and two target individuals to be compared.

We use AlphaSimR‘s pullIbdHaplo function to extract tracked founder haplotypes (see below) and then loop over chromosomes to apply the above comparison functions.

## Find shared segments between two target individuals in a
## population

compare_individuals <- function(pop,
                                target_individuals,
                                simparam) {

    n_chr <- simparam$nChr

    ind1_ix <- paste(target_individuals[1], c("_1", "_2"), sep = "")
    ind2_ix <- paste(target_individuals[2], c("_1", "_2"), sep = "")

    ibd <- pullIbdHaplo(pop,
                        simParam = simparam)

    map <- simparam$genMap
    loci_per_chr <- map_dbl(map, length)

    chr_ends <- cumsum(loci_per_chr)
    chr_starts <- c(1, chr_ends[-n_chr] + 1)

    results <- vector(mode = "list",
                      length = n_chr)

    for (chr_ix in 1:n_chr) {

        ind1 <- ibd[ind1_ix, chr_starts[chr_ix]:chr_ends[chr_ix]]
        ind2 <- ibd[ind2_ix, chr_starts[chr_ix]:chr_ends[chr_ix]]

        results[[chr_ix]] <- compare_individuals_chr(ind1, ind2, map[[chr_ix]])
        results[[chr_ix]]$chr <- chr_ix
    }

    bind_rows(results)
}

(You might think it would be more elegant, when looping over chromosomes, to pull out the identity-by-descent data for each chromosome at a time. This won’t work on version 1.0.4 though, because of a problem with pullIbdHaplo which has been fixed in the development version.)

We use an analogous function to compare the haplotypes carried by one individual. See the details on GitHub if you’re interested.

Building the simulation

We are ready to run our simulation: This code creates a few founder individuals that will initiate the pedigree, and sets up a basic simulation. The key simulation parameter is to set setTrackRec(TRUE) to turn on tracking of recombinations and founder haplotypes.

source("R/simulation_functions.R")

## Set up simulation

founders <- runMacs(nInd = 10,
                    nChr = 25)

simparam <- SimParam$new(founders)

simparam$setTrackRec(TRUE)

founderpop <- newPop(founders,
                     simParam = simparam)

To simulate a pedigree, we use pedigreeCross, a built-in function to simulate a given pedigree, and then apply our comparison functions to the resulting simulated population.

## Run the simulation for a pedigree one replicate

simulate_pedigree <- function(ped,
                              target_individuals,
                              focal_individual,
                              founderpop,
                              simparam) {
    pop <- pedigreeCross(founderPop = founderpop,
                         id = ped$id,
                         mother = ped$mother,
                         father = ped$father,
                         simParam = simparam)
    shared_parents <- compare_individuals(pop,
                                          target_individuals,
                                          simparam)
    shared_inbred <- compare_self(pop,
                                  focal_individual,
                                  simparam)
    list(population = pop,
         shared_segments_parents = shared_parents,
         shared_segments_self_inbred = shared_inbred)
}

Results

First we can check how large proportion of the genome of our inbred individuals is shared between their two haplotypes, averaged over 100 replicates. That is, how much of the genome is homozygous identical by descent — what is their genomic inbreeding? It lines up with the expectation form pedigree: 0.25 for the half-sib pedigree, close to 0.125 for the full-sib pedigree and close to 0.0625 for the cousin pedigree. The proportion shared by the parents is, as it should, about double that.

      case inbred_self_sharing parent_sharing
  full-sib        0.25 (0.052)    0.5 (0.041)
  half-sib        0.13 (0.038)   0.25 (0.029)
    cousin       0.064 (0.027)   0.13 (0.022)

Table of the mean proportion of genome shared between the two genome copies in inbred individuals and between their parents. Standard deviations in parentheses.

This is a nice consistency check, but not really what we wanted. The point of explicitly simulating chromosomes and recombinations is to look at segments, not just total sharing.

With a little counting and summarisation, we can plot the distributions of segment lengths. The horizontal axis is the length of the segments expressed in centimorgan. The vertical axis is the number of shared
segments of this length or longer. Each line is a replicate.

If we look at the summaries (table below), full-sibs share on average 74 segments greater than 1 cM in length, half-sibs 37, and cousins 29.

In real data, short segments might be harder to detect, but because we’re using simulated fake data, we don’t have to worry about phasing errors or false positive sharing.

If we look only at long segments (> 20 cM), full-sibs share on average 46 segments, half-sibs 23, and cousins 13. (Also, similar to Williams’ simulations, none of the cousins simulated here had less than five long segments shared.)

  case     `1 cM`   `10 cM`  `20 cM`  `30 cM`  `40 cM`  
  full-sib 74 (5.2) 60 (4.2) 46 (3.6) 34 (4)   24 (3.8) 
  half-sib 37 (3.4) 30 (3.1) 23 (3.3) 17 (2.8) 13 (2.6) 
  cousin   29 (3.8) 20 (3.3) 13 (3.2) 7.6 (2)  4.3 (1.8)

Table of the mean number of shared segments of different minimum length. Standard deviations in parentheses.

We an also look at the average length of the segments shared, and note that while full-sibs and half-sibs differ in the number of segments, and total segment length shared (above), the length of individual segments is about the same:

  case     mean_length_sd
  full-sib 0.33 (0.032)  
  half-sib 0.34 (0.042)  
  cousin   0.21 (0.03)

Table of the mean length shared segments. Standard deviations in parentheses.

Limitations

Williams’ simulation, using the ped-sim tool, had a more detailed model of recombination in the human genome, with different interference parameters for each chromosome, sex-specific recombination and so on. In that way, it is much more realistic.
We’re not modelling any one genome in particular, but a very generic genome. Each chromosome is 100 cM long for example; one can imagine that a genome with many short chromosomes would give a different distribution. This can be changed, though; the chromosome size is the easiest, if we just pick a species.

Literature

Yengo, L., Wray, N. R., & Visscher, P. M. (2019). Extreme inbreeding in a European ancestry sample from the contemporary UK population. Nature communications, 10(1), 1-11.

Qiao, Y., Sannerud, J. G., Basu-Roy, S., Hayward, C., & Williams, A. L. (2021). Distinguishing pedigree relationships via multi-way identity by descent sharing and sex-specific genetic maps. The American Journal of Human Genetics, 108(1), 68-83.

The hybrid online future

Without making any predictions about what will happen with the pandemic or when, I suspect that we are never going back to the way things were in terms of on-campus education and meetings. A lot more of university life will be hybrid online. This isn’t because hybrid online is necessarily great; I suspect that in terms of meetings, a hybrid meeting with some folks in a room and others on videoconference is the worst of two worlds. But it might be the best option that is possible — when an in-person meeting is better than a hybrid meeting, but a hybrid meeting is better than no meeting.

People get sick, at any time, and the prosocial thing to do is to stay at home and not spread the infection more than necessary. I expect, and hope, that this norm will remain, and we will have less people sick in class and at work. Students who fall ill will, reasonably, expect to be able to participate from home when they do the right thing and stay home from class. Teachers who suddenly fall ill likely expect it too. After all, it is less painful, for everyone involved, than cancelling and rescheduling.

If we are reasonable and empathetic, we will accommodate. If I’m right that hybrid meetings are, in general, slightly worse than in person meetings, the meeting quality will on average be worse — but more people will be able to participate, and that is also valuable. So it might not feel like it, but taken together, the hybrid solution might be better. The exact balance would depend on how much worse or better different meeting forms are; we probably can’t put numbers on that.

The same argument applies to online scientific conferences. I can’t imagine that the online conference experience is as useful, inspiring and conducive to networking as an in-person conference. My personal impression is that online conferences and seminars are great for watching talks, but bad for meeting people. However, online conferences are accessible to more people — those who for some reason can’t travel, can’t afford it, can’t be away from home for that long.

We might not feel excited about it, but the hybrid online future is here.

2021 blog recap

Dear diary,

Time for the meta-post of the year! During 2021, the blog racked up 28 posts (counting this one), about the same pace as 2020. That’s okay.

As usual, let’s pick one post a month to represent the blogging year of 2021:

January: A model of polygenic adaptation in an infinite population. We look at some equations and make two animations following Jain & Stephan (2017).

February: The Fulsom Principle: Smart people will gladly ridicule others for breaking supposed rules that are in fact poorly justified.

March: Theory in genetics. As I’m using more modelling in my work, here is some inspiration from an essay by Brian Charlesworth. As I hadn’t read Guest & Martin (2021) at the time, the post only cites Robinaugh at al. (2020) and music theory youtuber Adam Neely, and that’s also quite good.

April: Researchers in ecology and evolution don’t use Platt’s strong inference, and that’s okay. This post is reacting to a paper that advocates explicit hypotheses in evolution and ecology, a paper I think qualifies as ”wrong, but wrong in an interesting and productive way” (can’t remember who said that).

Also, this post also got one of the coveted Friday Links mentions on Dynamic Ecology, before it shut down. End of an era, death of blogs etc.

May: Convincing myself about the Monty Hall problem Probably my favourite post of the year. It also shows the value of a physical model: I had what felt like the crucial moment that made the problem click as I was physically acting out Monty Hall choices with myself. Also, first shout-out to Guest & Martin (2021), a paper that will be cited again on the blog, I’m sure. I think the Monty Hall problem is a great example of their claim that a precise mathematical theory can’t defeat intuition unless you run the numbers and do the calculations.

June: no posts, distracted by work and pandemic, I guess.

July: Journal club of one: ”A unifying concept of animal breeding programmes”. Rather long post about a paper about a graphical method for displaying simulated breeding structures, and whether this qualifies as a formal specification or not.

August: ”Dangerous gene myths abound” , reacting to an article by Philip Ball. The breathless hype around genomics is often embarrassing, but criticisms of reductionism in genetics love attacking caricatures.

September: Belief in science, some meditations on how little it knows and how science ”works whether you believe in it or not”

October–November: extended blog vacation

December: Well, there are only two to choose from, but the other day I posted some notes about two methods that try to infer recent population history from linkage disequilibrium.

Outwith the blog, there were also some papers published. I’m really behind on giving them their own blog posts, but that might be rectified in time. The blog runs on its own schedule where papers remain ”recent” for several years.

• Johnsson M, Wall H, Lopes Pinto FA, Fleming RH, McCormack HA, Benavides-Reyes C, Dominguez-Gasca N, Sanchez-Rodriguez E, Dunn IC, Rodriguez-Navarro AB, Kindmark A, de Koning D-J. Genetics of tibia bone properties of crossbred commercial laying hens in different housing systems. Preprint. (Blog post)
• Johnsson M, Wahlen A, Ros-Freixedes R, Gorjanc G, Chen C-Y, Herring WO, de Koning D-J, Hickey JM. Genetic variation in recombination rate in the pig. Genetics Selection Evolution. (Blog post.)
• Johnsson M, Henriksen R, Wright D. The neural crest cell hypothesis: no unified explanation for domestication. Genetics. We examine the genomic evidence for the popular neural crest cell hypothesis of domestication, and find it lacking.
• Johnsson M, Jungnickel, MK. Evidence for and localization of proposed causative variants in cattle and pig genomes. Genetics Selection Evolution. Reviewing causative variants in farm animals, and thinking of what to do to find more of them.
• Powell O, Mrode R, Gaynor RC, Johnsson M, Gorjanc G, Hickey JM. Genomic evaluations using data recorded on smallholder dairy farms in low- to middle-income countries. JDS Communcations.
• Gozalo-Marcilla M, Buntjer J, Johnsson M, Batista L, Diez F, Werner CR, Chen C-Y, Gorjanc G, Mellanby RJ, Hickey JM, Ros-Freixedes R. (2021). Genetic architecture and major genes for backfat thickness in pig lines of diverse genetic backgrounds. Genetics Selection Evolution.
• Dadousis C, Somavilla A, Ilska JJ, Johnsson M, Batista L, Mellanby RJ, Headon D, Gottardo P, Whalen A, Wilson D, Dunn IC, Gorjanc G, Kranis A, Hickey JM. A genome-wide association analysis for body weight at 35 days measured on 137,343 broiler chickens. Genetics Selection Evolution.
• Fallahshahroudi A, Johnsson M, Sorato E, Ubhayasekera SJ, Bergquist J, Altimiras J, Jensen P. Effects of the Domestic Thyroid Stimulating Hormone Receptor (TSHR) Variant on the Hypothalamic—Pituitary—Thyroid Axis and Behavior in Chicken. Genetics.

What else is new? Astute readers may have noticed that my job description has changed from ”postdoc” to ”researcher”. Now, ”researcher” is a little bit of an ambiguous title because some institutions also use it for time limited positions — but no, dear reader, I am now permanently employed at the Department of Animal Breeding and Genetics, Swedish University of Agricultural Sciences where, among other things, I lead the ”Genome dynamics of livestock breeding” project financed by the research council Formas. This will be great fun, and also show on the blog in time, I’m sure.

Belief in science

It can be a touchy topic whether people who do science or make use of outcomes of science are supposed to believe in science. I can think of at least three ways that we may or may not believe in science.

Knowledge tunnels

Imagine that we try to apply the current state of scientific knowledge to some everyday occurrence. It could be something that happens when cooking, a very particular sensation you notice in your body, anything that you have practical experience-based knowledge about, one of those particular phenomena that anyone notices when in some practical line of work. Every trade has its own specialised terminology and models of explanation that develops based on experience.

When looking closely, we will often find that the current state of scientific knowledge does not have a theory, model or explanation ready for us. This might not be because the problem is so hard to be unsolvable. It might be because the problem has simply been overlooked.

That means that if we want to maintain a world view where science has the answer, we don’t just need to believe in particular statements that science makes. We also need to trust that a scientific explanation can be developed for many cases where one doesn’t exist yet.

I can’t remember who I read who used this image (I think it might have been a mathematician): knowledge is not a solid body of work, but more like tunnels dug out of the mostly unknown. We don’t know most things, but we know some paths dug through this mass.

Whether you believe in it or not

There is another popular saying: the good thing about it is that it works whether you believe in it or not — said by Neil DeGrasse Tyson about science and attributed to Niels Bohr about superstition.

This seems to be true, not just about deep cases such as keeping one set of methodological assumptions for your scientific work and another, say a deeply spiritual religious one, for your personal life. It seems to be true about the way we expect scientists to work and communicate on an everyday level. Scientists do not need to be committed to every statement in their writing or every hypothesis they pursue.

Dang & Bright (2021) ask what demands we should put on individual scientific contributions (e.g. journal articles). They consider assertion norms, the idea that certain types of utterances are appropriate for a certain context, and argue that scientific contributions should not be held to these norms. That is, scientific claims need not be something the researcher knows, has justification for, or believes.

They give an example of a scientist who comes up with a new hypothesis, and performs some research that supports it. Overall, however, the literature does not support it. The scientist publishes a paper advocating for the hypothesis. In a few years, further research demonstrates that it is false. They suggest that in this case, the scientist has done what we expect scientists to do, even if:

• The claims are not accurate; they are false.
• The claims are not justified, in the sense that they do not have the support of the wider literature, and the data do not conclusively support the hypothesis.
• The scientist did not fully believe the claims.

They try to explain these norms of communication with reference to how the scientific community learns. They argue that this way of communicating facilitates an intellectual division of labour: different researchers consider different ideas and theories, that might at times be at odds, and therefore there is value to allowing them to them saying conflicting things.

The rejected norms were picked as the basis of our inquiry since they had been found plausible or defensible as norms for assertion, which is at least a somewhat related activity of putting forward scientific public avowals. So why this discrepancy? In short, we think this is because the social enterprise of inquiry requires that we allow people to be more lax in certain contexts than we normally require of individuals offering testimony, and through a long process of cultural evolution the scientific community developed norms of avowal to accommodate that fact.

Another reason, pragmatically, why scientists might not be fully committed to everything they’ve written is that, at least in natural science, writing often happens by committee. And not just a committee of co-authors, but also by reviewers and editors, who also take part in negotiations about what can be claimed in any piece of peer reviewed writing. Yes, there are people who like to say that every co-author needs to be able to take full responsibility for everything written — but the real lowest common denominator seems that none of the co-authors objects too much to what is written.

Weak citations

Finally, there appears to be two ways to think about claims when reading or writing scientific papers, that may explain that researchers can be at the same time highly critical of some claims, and somewhat credulous about other claims. Think of your typical introduction to an empirical paper, which will often have citations in passing to stylised facts that are taken to be true, but not explored at any depth — those ”neutral citations” that some think are shallow and damaging. Does that mean that scientists are lazy about the truth, just believing the first thing they see and jumping on citation bandwagons? Maybe. Because there is no other way they could write, really.

When we read or write about science, we have to divide claims into those that are currently under critical scrutiny, and those that are currently considered background. If we believe Quine, there isn’t an easy way to separate these two types of ideas, no logical division into hypothesis proper and auxiliary assumption. But we still need to make it, possibly in an arbitrary way, unless we want our research project to be an endless rabbit hole of questions. This does not mean that we have to believe the background claims in any deeper sense. They might be up for scrutiny tomorrow.

This is another reason why it’s a bad idea to try to learn a field by reading the introductions to empirical papers. Introductions are not critical expositions that synthesise evidence and give the best possible view of the state of the field. They just try to get the important background out of the way so we can move on with the work at hand.

Literature

Dang, H., & Bright, L. K. (2021). Scientific conclusions need not be accurate, justified, or believed by their authors. Synthese.

”Dangerous gene myths abound”

Philip Ball, who is a knowledgeable and thoughtful science writer, published an piece in the Guardian a couple of months ago about the misunderstood legacy of the human genome project: ”20 years after the human genome was first sequenced, dangerous gene myths abound”.

The human genome project published the draft reference genome for the human species 20 years ago. Ball argues, in short, that the project was oversold with promises that it couldn’t deliver, and consequently has not delivered. Instead, the genome project was good for other things that had more to do with technology development and scientific infrastructure. The sequencing of the human genome was the platform for modern genome science, but it didn’t, for example, cure cancer or uncover a complete set of instructions for building a human.

He also argues that the rhetoric of human genome hype, which did not end with the promotion of the human genome project (see the ENCODE robot punching cancer in the face, for example), is harmful. It is scientifically harmful because it oversimplifies modern genetics, and it is politically harmful because it aligns well with genetic determinism and scientific racism.

I believe Ball is entirely right about this.

Selling out

The breathless hype around the human genome project was embarrassing. Ball quotes some fragments, but you can to to the current human genome project site and enjoy quotes like ”it’s a transformative textbook of medicine, with insights that will give health care providers immense new powers to treat, prevent and cure disease”. This image has some metonymical truth to it — human genomics is helping medical science in different ways — but even as a metaphor, it is obviously false. You can go look at the human reference genome if you want, and you will discover that the ”text” such as it is looks more like this than a medical textbook:

TTTTTTTTCCTTTTTTTTCTTTTGAGATGGAGTCTCGCTCTGCCGCCCAGGCTGGAGTGC
AGTAGCTCGATCTCTGCTCACTGCAAGCTCCGCCTCCCGGGTTCACGCCATTCTCCTGCC
TCAGCCTCCTGAGTAGCTGGGACTACAGGCGCCCACCACCATGCCCAGCTAATTTTTTTT
TTTTTTTTTTTGGTATTTTTAGTAGAGACGGGGTTTCACCGTGTTAGCCAGGATGGTCTC
AATCTCCTGACCTTGTGATCCGCCCGCCTCGGCCTCCCACAGTGCTGGGATTACAGGC

This is a human Alu element from chromosome 17. It’s also in an intron of a gene, flanking a promoter, a few hundred basepairs away from an insulator (see the Ensembl genome browser) … All that is stuff that cannot be read from the sequence alone. You might be able to tell that it’s Alu if you’re an Alu genius or run a sequence recognition software, but there is no to read the other contextual genomic information, and there is no way you can tell anything about human health by reading it.

I think Ball is right that this is part of simplistic genetics that doesn’t appreciate the complexity either quantitative or molecular genetics. In short, quantitative genetics, as a framework, says that inheritance of traits between relatives is due to thousands and thousands of genetic differences each of them with tiny effects. Molecular genetics says that each of those genetic differences may operate through any of a dizzying selection of Rube Goldberg-esque molecular mechanisms, to the point where understanding one of them might be a lifetime of laboratory investigation.

Simple inheritance is essentially a fiction, or put more politely: a simple model that is useful as a step to build up a more better picture of inheritance. This is not knew; the knowledge that everything of note is complex has been around since the beginning of genetics. Even rare genetic diseases understood as monogenic are caused by sometimes thousands of different variants that happen in a particular small subset of the genome. Really simple traits, in the sense of one variant–one phenotype, seldom happen in large mixing and migrating populations like humans; they may occur in crosses constructed in the lab, or in extreme structured populations like dog breeds or possibly with balancing selection.

Can you market thick sequencing?

Ball is also right about what it was most useful about the human genome project: it enabled research at scale into human genetic variation, and it stimulated development of sequencing methods, both generating and using DNA sequence. Lowe (2018) talks about ”thick” sequencing, a notion of sequencing that includes associated activities like assembly, annotation and distribution to a community of researchers — on top of ”thin” sequencing as determination of sequences of base pairs. Thick sequencing better captures how genome sequencing is used and stimulates other research, and aligns with how sequencing is an iterative process, where reference genomes are successively refined and updated in the face of new data, expert knowledge and quality checking.

It is hard to imagine gene editing like CRISPR being applied in any human cell without a good genome sequence to help find out what to cut out and what to put instead. It is hard to imagine the developments in functional genomics that all use short read sequencing as a read-out without having a good genome sequence to anchor the reads on. It is possible to imagine genome-wide association just based on very dense linkage maps, but it is a bit far-fetched. And so on.

Now, this raises a painful but interesting question: Would the genome project ever have gotten funded on reasonable promises and reasonable uncertainties? If not, how do we feel about the genome hype — necessary evil, unforgivable deception, something in-between? Ball seems to think that gene hype was an honest mistake and that scientists were surprised that genomes turned out to be more complicated than anticipated. Unlike him, I do not believe that most researchers honestly believed the hype — they must have known that they were overselling like crazy. They were no fools.

An example of this is the story about how many genes humans have. Ball writes:

All the same, scientists thought genes and traits could be readily matched, like those children’s puzzles in which you trace convoluted links between two sets of items. That misconception explains why most geneticists overestimated the total number of human genes by a factor of several-fold – an error typically presented now with a grinning “Oops!” rather than as a sign of a fundamental error about what genes are and how they work.

This is a complicated history. Gene number estimates are varied, but enjoy this passage from Lewontin in 1977:

The number of genes is not large

While higher organisms have enough DNA to specify from 100,000 to 1,000,000 proteins of average size, it appears that the actual number of cistrons does not exceed a few thousand. Thus, saturation lethal mapping of the fourth chromosome (Hochman, 1971) and the X chromosome (Judd, Shen and Kaufman, 1972) of Drosophila melanogbaster make it appear that there is one cistron per salivary chromosome band, of which there are 5,000 in this species. Whether 5,000 is a large or small number of total genes depends, of course, on the degree of interaction of various cistrons in influencing various traits. Nevertheless, it is apparent that either a given trait is strongly influenced by only a small number of genes, or else there is a high order of gene interactions among developmental systems. With 5,000 genes we cannot maintain a view that different parts of the organism are both independent genetically and each influenced by large number of gene loci.

I don’t know if underestimating by an few folds is worse than overestimating by a few folds (D. melanogaster has 15,000 protein-coding genes or so), but the point is that knowledgeable geneticists did not go around believing that there was a simple 1-to-1 mapping between genes and traits, or even between genes and proteins at this time. I know Lewontin is a population geneticist, and in the popular mythology population geneticists are nothing but single-minded bean counters who do not appreciate the complexity of molecular biology … but you know, they were no fools.

The selfish cistron

One thing Ball gets wrong is evolutionary genetics, where he mixes genetic concepts that, really, have very little to do with each other despite superficially sounding similar.

Yet plenty remain happy to propagate the misleading idea that we are “gene machines” and our DNA is our “blueprint”. It is no wonder that public understanding of genetics is so blighted by notions of genetic determinism – not to mention the now ludicrous (but lucrative) idea that DNA genealogy tells you which percentage of you is “Scots”, “sub-Saharan African” or “Neanderthal”.

This passage smushes two very different parts of genetics together, that don’t belong together and have nothing to do with with the preceding questions about how many genes there are or if the DNA is a blueprint: The gene-centric view of adaptation, a way of thinking of natural selection where you imagine genetic variants (not organisms, not genomes, not populations or species) as competing for reproduction; and genetic genealogy and ancestry models, where you describe how individuals are related based on the genetic variation they carry. The gene-centric view is about adaptation, while genetic genealogy works because of effectively neutral genetics that just floats around, giving us a unique individual barcode due to the sheer combinatorics.

He doesn’t elaborate on the gene machines, but it links to a paper (Ridley 1984) on Williams’ and Dawkins’ ”selfish gene” or ”gene-centric perspective”. I’ve been on about this before, but when evolutionary geneticists say ”selfish gene”, they don’t mean ”the selfish protein-coding DNA element”; they mean something closer to ”the selfish allele”. They are not committed to any view that the genome is a blueprint, or that only protein-coding genes matter to adaptation, or that there is a 1-to-1 correspondence between genetic variants and traits.

This is the problem with correcting misconceptions in genetics: it’s easy to chide others for being confused about the parts you know well, and then make a hash of some other parts that you don’t know very well yourself. Maybe when researchers say ”gene” in a context that doesn’t sound right to you, they have a different use of the word in mind … or they’re conceptually confused fools, who knows.

Literature

Lewontin, R. C. (1977). The relevance of molecular biology to plant and animal breeding. In International Conference on Quantitative Genetics. Ames, Iowa (USA). 16-21 Aug 1976.

Lowe, J. W. (2018). Sequencing through thick and thin: Historiographical and philosophical implications. Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences, 72, 10-27.

Using R: plyr to purrr, part 1

This is the second post about my journey towards writing more modern Tidyverse-style R code; here is the previous one. We will look at the common case of taking subset of data out of a data frame, making some complex R object from them, and then extracting summaries from those objects.

More nostalgia about plyr

I miss the plyr package. Especially ddply, ldply, and dlply, my favourite trio of R functions of all times. Yes, the contemporary Tidyverse package dplyr is fast and neat. And those plyr functions operating on arrays were maybe overkill; I seldom used them. But plyr was so smooth, so beautiful, and — after you’ve bashed your head against it for some time and it changed your mind — so intuitive. The package still exists, but it’s retired, and we shouldn’t keep writing R code like it’s 2009, should we?

I used to like to do something like this: take a data frame, push it through a function that returns some complex object, store those objects in a list, and then map various functions over that list to extract the parts I care about. What is the equivalent in the new idiom? To do the same thing but with the purrr package, of course! purrr replaces the list-centric parts of plyr, while dplyr covers data frame-centric summarisation, mutation and so on.

For this example we will be using the lm function on subsets of data and store the model object. It’s the simple case that everyone reaches for to demonstrate these features, but it’s a bit dubious. If you find yourself fitting a lot of linear models to subsets, maybe there are other models you should think about Especially here, when the fake data just happens to come from a multilevel model with varying intercepts … But in this case, let’s simulate a simple linear regression and look at the coefficients we get out.

set.seed(20210807)

n_groups <- 10
group_sizes <- rpois(n_groups, 10)
n <- sum(group_sizes)

fake_data <- tibble(id = 1:n,
                    group = rep(1:n_groups,
                                times = group_sizes),
                    predictor = runif(n, 0, 1))
group_intercept <- rnorm(n_groups, 0, 1)

fake_data$response <- fake_data$predictor * 10 +
  group_intercept[fake_data$group] +
  rnorm(n)

And here is the plyr code: First, dlply takes us from a data frame, splitting it by group, to a list of linear models. Then, ldply takes us from the list of models to a data frame of coefficients. tidy is a function from the wonderful broom package which extracts the same information as you would get in the rather unwieldy object from summary(lm), but as a data frame.

library(plyr)
library(broom)

fit_model <- function(data) {
  lm(response ~ predictor, data)
}

models <- dlply(fake_data,
                     "group",
                     fit_model)
result <- ldply(models, tidy)

This is what the results might looks like. Notice how ldply adds the split labels nicely into the group column, so we know which rows came from which subset.

   group        term   estimate std.error  statistic      p.value
1      1 (Intercept) -0.2519167 0.5757214 -0.4375670 6.732729e-01
2      1   predictor 10.6136902 1.0051490 10.5593207 5.645878e-06
3      2 (Intercept)  3.1528489 0.6365294  4.9531864 7.878498e-04
4      2   predictor  8.2075766 1.1458702  7.1627452 5.292586e-05
5      3 (Intercept) -0.8103777 0.6901212 -1.1742542 2.786901e-01
...

split/map: The modern synthesis

If we pull out purrr, we can get the exact same table like so. The one difference is that we get a tibble (that is, a contemporary, more well-behaved data frame) out of it instead of a base R data.frame.

library(purrr)

models <- map(split(fake_data,
                    fake_data$group),
                    fit_model)
result <- map_df(models,
                 tidy,
                 .id = "group")

# A tibble: 80 x 6
   group term        estimate std.error statistic  p.value
                            
 1 1     (Intercept)     1.67     0.773      2.16 6.32e- 2
 2 1     predictor       8.67     1.36       6.39 2.12e- 4
 3 2     (Intercept)     4.11     0.566      7.26 4.75e- 5
 4 2     predictor       8.19     1.11       7.36 4.30e- 5
 5 3     (Intercept)    -7.50     0.952     -7.89 9.99e- 5
 6 3     predictor      11.5      1.75       6.60 3.03e- 4
 7 4     (Intercept)   -19.8      0.540    -36.7  7.32e-13
 8 4     predictor      11.5      0.896     12.8  5.90e- 8
 9 5     (Intercept)   -12.4      1.03     -12.0  7.51e- 7
10 5     predictor       9.69     1.82       5.34 4.71e- 4
# … with 70 more rows

First, the base function split lets us break the data into subsets based on the values of a variable, which in this case is our group variable. The output of this function is a list of data frames, one for each group.

Second, we use map to apply a function to each element of that list. The function is the same modelling function that we used above, which shoves the data into lm. We now have our list of linear models.

Third, we apply the tidy function to each element of that list of models. Because we want the result to be one single data frame consolidating the output from each element, we use map_df, which will combine the results for us. (If we’d just use map again, we would get a list of data frames.) The .id argument tells map to add the group column that indicates what element of the list of models each row comes from. We want this to be able to identify the coefficients.

If we want to be fancy, we can express with the Tidyverse-related pipe and dot notation:

library(magrittr)

result <- fake_data %>%
  split(.$group) %>%
  map(fit_model) %>%
  map_df(tidy, .id = "group")

Nesting data into list columns

This (minus the pipes) is where I am at in most of my R code nowadays: split with split, apply with map and combine with map_dfr. This works well and looks neater than the lapply/Reduce solution discussed in part 0.

We can push it a step further, though. Why take the linear model out of the data frame, away from its group labels any potential group-level covariates — isn’t that just inviting some kind of mix-up of the elements? With list columns, we could store the groups in a data frame, keeping the data subsets and any R objects we generate from them together. (See Wickham’s & Grolemund’s R for Data Science for a deeper case study of this idea.)

library(dplyr)
library(tidyr)

fake_data_nested <- nest(group_by(fake_data, group),
                         data = c(id, predictor, response))

fake_data_models <- mutate(fake_data_nested,
                           model = map(data,
                                       fit_model),
                           estimates = map(model,
                                           tidy))

result <- unnest(fake_data_models, estimates)

First, we use the nest function to create a data frame where each row is a group, and the ”data” column contains the data for that subset.

Then, we add two list columns to that data frame: our list of models, and then our list of data frames with the coefficients.

Finally, we extract the estimates into a new data frame with unnest. The result is the same data frame of coefficients and statistics, also carrying along the data subsets, linear models and coefficents.

The same code with pipes:

fake_data %>% 
  group_by(group) %>% 
  nest(data = c(id, predictor, response)) %>% 
  mutate(model = map(data, fit_model),
         estimates = map(model, tidy)) %>% 
  unnest(estimates) -> ## right way assignment just for kicks
  result

I’m still a list column sceptic, but I have to concede that this is pretty elegant. It gets the job done, it keeps objects that belong together together so that there is no risk of messing up the order, and it is not that much more verbose. I especially like that we can run the models and extract the coefficients in the same mutate call.

Coda: mixed model

Finally, I can’t resist comparing the separate linear models to a linear mixed model of all the data.

We use lme4 to fit a varying-intercept model, a model that puts the same coefficient on the slope between the response and predictor in each group, but allows the intercepts to vary between groups, assuming them to be drawn from the same normal distribution. We put the coefficients from the linear models fit in each group separately and the linear mixed model together in the same data frame to be able to plot them.

library(ggplot2)
library(lme4)

model <- lmer(response ~ (1|group) + predictor,
              fake_data)

lm_coef <- pivot_wider(result,
                       names_from = term,
                       values_from = estimate,
                       id_cols = group)

lmm_coef <- cbind(group = levels(model@flist$group),
                  coef(model)$group)

model_coef <- rbind(transform(lm_coef, model = "lm"),
                    transform(lmm_coef, model = "lmm"))

colnames(model_coef)[2] <- "intercept"

ggplot() +
  geom_point(aes(x = predictor,
                 y = response,
                 colour = factor(group)),
             data = fake_data) +
  geom_abline(aes(slope = predictor,
                  intercept = intercept,
                  colour = factor(group),
                  linetype = model),
              data = model_coef) +
  theme_bw() +
  theme(panel.grid = element_blank())

As advertised, the linear mixed model has the same slope in every group, and intercepts pulled closer to the mean. Now, we know that this is a good model for these fake data because we created them, and in the real world, that is obviously not the case … The point is: if we are going to fit a more complex model of the whole data, we want to be able to explore alternatives and plot them together with the data. Having elegant ways to transform data frames and summarise models at our disposal makes that process smoother.

”It depends on what you want to do with it”

Note to self: ”It depends on what you want to do with it” is the stereotypical answer to questions about method and data analysis. Ask what genetic analysis software you should use to do X, how you should filter the variants you’ve detected from sequencing, whether to mark duplicates on your aligned reads, what a genetic parameter estimate means … I just wrote a version of this answer in an email. Mea maxima culpa.

Admittedly, it is probably often the technically correct answer, but it’s also useless without qualification. It always depends. Everything is everything-dependent. Goddag yxskaft. Moreover, I suspect that it often means ”I don’t know” or ”it doesn’t matter” — but you can’t say that, can you? That would sound unprofessional.

Here is what to ask either the supposed expert who blurted out this non-answer, or yourself if you are about to: What are the alternatives? A couple will do to give an idea of what the field of solutions and answers is like. What does it depend on? An idea of why one want to choose one alternative over the other will do. What do we need to know? Sometimes we need preliminary data, a huge modelling effort … or just that I go read some papers before I say anything more.

Journal club of one: ”A unifying concept of animal breeding programmes”

The developers of the MoBPS breeding programme simulators have published three papers about it over the last years: one about the MoBPS R package (Pook et al. 2020), one about their web server MoBPSweb (Pook et al. 2021), and one that discusses the logic of the specification for breeding programmes they use in the web interface (Simianer et al. 2021). The idea is that this specification can be used to describe breeding programmes in a precise and interoperable manner. The latter — about breeding programme specification — reads as if the authors had a jolly good time thinking about what breeding and breeding programmes are; at least, I had such feelings while reading it. It is accompanied by an editorial by Simianer (2021) talking about what he thinks are the important research directions for animal breeding research. Using simulation to aid breeding programme design is one of them.

Defining and specifying breeding programmes

After defining a breeding programme in a narrow genetic sense as a process achieving genetic change (more about that later), Simianer et al. (2021) go on to define a specification of such a breeding programme — or more precisely, of a model of a breeding programme. They use the word ”definition” for both things, but they really talk about two different things: defining what ”a breeding programme” is and specifying a particular model of a particular breeding programme.

Here, I think it is helpful to think of Guest & Martin’s (2020) distinction, borrowed from psychology, between a specification of a model and an implementation of a model. A specification is a description of a model based in natural language or math. Breeding programme modelling often takes the shape of software packages, where the software implementation is the model and a specification is quite vague. Simianer et al. (2021) can be seen as a step towards a way of writing specifications, on a higher level in Guest & Martin’s hierarchy, of what such a breeding programme model should achieve.

They argue that such a specification (”formal description”) needs to be comprehensive, unambiguous and reproducible. They claim that this can be achieved with two parts: the breeding environment and the breeding structure.

The breeding environment includes:

• founder populations,
• quantitative genetic parameters for traits,
• genetic architectures for traits,
• economic values for traits in breeding goal,
• description of genomic information,
• description of breeding value estimation methods.

Thus, the ”formal” specification depends on a lot of information that is either unknowable in practice (genetic architecture), estimated with error (genetic parameters), hard to describe other than qualitatively (founder population) and dependent on particular software implementations and procedures (breeding value estimation). This illustrates the need to distinguish the map from the territory — to the extent that the specification is exact, it describes a model of a breeding programme, not a real breeding programme.

The other part of their specification is the graph-based model of breeding structure. I think this is their key new idea. The breeding structure, in their specification, consists of nodes that represent groups of elementary objects (I would say ”populations”) and edges that represent transformations that create new populations (such as selection or mating) or are a shorthand for repeating groups of edges and nodes.

The elementary objects could be individuals, but they also give the example of gametes and genes (I presume they mean in the sense of alleles) as possible elementary objects. One could also imagine groups of genetically identical individuals (”genotypes” in a plant breeding sense). Nodes contain a given number of individuals, and can also have a duration.

Edges are directed, and correspond to processes such as ageing, selection, reproduction, splitting or merging populations. They will carry attributes related to the transformation. Edges can have a time associated with them that it takes for the transformation to happen (e.g. for animals to gestate or grow to a particular age). Here is an example from Pook et al. (2021) of a breeding structure graph for dairy cattle:

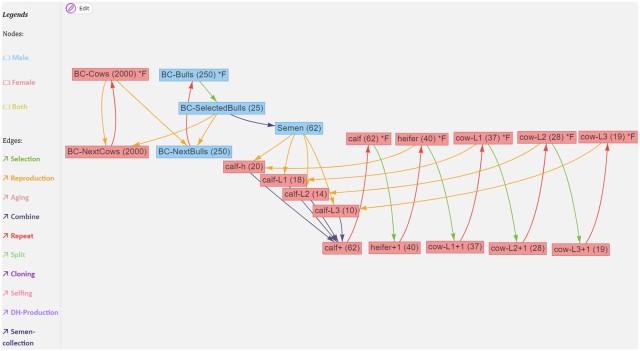
If we ignore the red edges for now, we can follow the flow of reproduction (yellow edges) and selection (green edges): The part on the left is what is going on in the breeding company: cows (BC-Cows) reproduce with selected bulls (BC-SelectedBulls), and their offspring become the next generation of breeding company cows and bulls (BC-NextCows and BC-NextBulls). On the right is the operation of a farm, where semen from the breeding company is used to inseminate cows and heifers (heifer, cow-L1, cow-L2, cow-L3) to produce calfs (calf-h, calf-L1, calf-L2, calf-L3). Each cycle each of these groups, through a selection operation, give rise to the next group (heifers becoming cows, first lactation cows becoming second lactation cows etc).

Breeding loops vs breeding graphs vs breeding forms

Except for the edges that specify breeding operations, there is also a special meta-edge type, the repeat edge, that is used to simplify breeding graphs with repeated operations.

A useful edge class to describe breeding programmes that are composed of several breeding cycles is ”repeat.” It can be used to copy resulting nodes from one breeding cycle into the nodes of origin of the next cycle, assuming that exactly the same breeding activities are to be repeated in each cycle. The “repeat” edge has the attribute “number of repeats” which allows to determine the desired number of cycles.

In the MoBPSweb paper (Pook et al. 2020), they describe how it is implemented in MoBPS: Given a breeding specification in MoBPSweb JSON format, the simulator will generate a directed graph by copying the nodes on the breeding cycle as many times as is specified by the repeat number. In this way, repeat edges are eliminated to make the breeding graph acyclic.

The conversion of the breeding scheme itself is done by first detecting if the breeding scheme has any “Repeat” edges (Simianer et al. 2020), which are used to indicate that a given part of the breeding programme is carried out multiple times (breeding cycles). If that is the case, it will subsequently check which nodes can be generated without the use of any repeat. Next, all repeats that can be executed based on the already available nodes are executed by generating copies of all nodes between the node of origin and the target node of the repeat (including the node of origin and excluding the target node). Nodes generated via repeat are serial-numbered via “_1,” “_2” etc. to indicate the repeat number. This procedure is repeated until all repeat edges are resolved, leading to a breeding programme without any repeats remaining.

There are at least three ways to specify the breeding structures for breeding programme simulations: these breeding graphs, breeding loops (or more generally, specifying breeding in a programming language) and breeding forms (when you get a pre-defined breeding structure and are allowed fill in the numbers).

If I’m going to compare the graph specification to what I’m more familiar with, this is how you would create a breeding structure in AlphaSimR:

library(AlphaSimR)

## Breeding environment

founderpop <- runMacs(nInd = 100,
                      nChr = 20)
simparam <- SimParam$new(founderpop)
simparam$setSexes("yes_sys")
simparam$addTraitA(nQtlPerChr = 100)
simparam$setVarE(h2 = 0.3)

## Breeding structure

n_time_steps <- 10

populations <- vector(mode = "list",
                      length = n_time_steps + 1)

populations[[1]] <- newPop(founderpop,
                           simParam = simparam)

for (gen_ix in 2:(n_time_steps + 1)) {

  ## Breeding cycle happens here

}

In the AlphaSimR script, the action typically happens within the loop. You apply different functions on population objects to make your selection, move individuals between parts of the breeding programme, create offspring etc. That is, in the MoBPS breeding structure, populations are nodes and actions are edges. In AlphaSimR, populations are objects and operations are functions. In order to not have to copy paste your breeding code, you use the control flow structures of R to make a loop (or some functional equivalent). In MoBPS graph structure, in order to not have to create every node and edge manually, you use the Repeat edge.

Breeding graphs with many repeat edges with different times attached to them have the potential to be complicated, and the same is true of breeding loops. I would have to use both of them more to have an opinion about what is more or less intuitive.

Now that we’ve described what they do in the paper, let’s look at some complications.

Formal specifications only apply to idealised breeding programmes

The authors claim that their concept provides a formal breeding programme specification (in their words, ”formal description”) that can be fully understood and implemented by breeders. It seems like the specification fails to live up to this ambition, and it appears doubtful whether any type of specification can. This is because they do not distinguish between specifying a model of a breeding programme and specifying a real implementation of a breeding programme.

First, as mentioned above, the ”breeding environment” as described by them, contains information that can never be specified for any real population, such as the genetic architecture of complex traits.

Second, their breeding structure is described in terms of fixed numbers, which will never be precise due to mortality, conception rates, logistics and practical concerns. They note such fluctuations in population size as a limitation in the Discussion. To some extent, random mortality, reproductive success etc an be modelled by putting random distributions on various parameters. (I am not sure how easy this is to do in the MoBPS framework; it is certainly possible.) However, this adds uncertainty about what these hyperparameter should be and whether they are realistic.

Such complications would just be nit-picking if the authors had not suggested that their specification can be used to communicate breeding programmes between breeders and between breeders and authorities, such as when a breeding programme is seeking approval. They acknowledge that the authorities, for example in the EU, want more detailed information that are beyond the scope of their specification.

And the concept is not very formal in the first place

Despite the claimed formality, every class of object in the breeding structure is left open, with many possible actions and many possible attributes that are never fully defined.

It is somewhat ambiguous what is to be the ”formal” specification — it cannot be the description in the paper as it is not very formal or complete; it shouldn’t be the implementation in MoBPS and MoBPSweb, as the concept is claimed to be universal; maybe it is the JSON specification of the breeding structure and background as described in the MoBPSweb paper (Pook et al. 2020). The latter seems the best candidate for a well-defined formal way to specify breeding programme models, but then again, the JSON format appears not to have a published specification, and appears to contain implementation-specific details relating to MoBPS.

This also matters to the suggested use of the specification to communicate real breeding programme designs. What, precisely, is it that will be communicated? Are breed societies and authorities expected to communicate with breeding graphs, JSON files, or with verbal descriptions using their terms (e.g. ”breeding environment”, ”breeding structure”, their node names and parameters for breeding activities)?

There is almost never a need for a definition

As I mentioned before, the paper starts by asking what a breeding programme is. They refer to different descriptions of breeding programme design from textbooks, and a legal definition from EU regulation 2016/1012; article 2, paragraph 26, which goes:

‘breeding programme’ means a set of systematic actions, including recording, selection, breeding and exchange of breeding animals and their germinal products, designed and implemented to preserve or enhance desired phenotypic and/or genotypic characteristics in the target breeding population.

There seems to be some agreement that a breeding programme, in addition to being the management of reproduction of a domestic animal population, also is systematic and goal-directed activity. Despite these descriptions of breeding programmes and their shared similarity, the authors argue that there is no clear formal definition of what a breeding programme is, and that this would be useful to delineate and specify breeding programmes.

They define a breeding programme as an organised process that aims to change the genetic composition in a desired direction, from one group of individuals to a group of individuals at a later time. The breeding programme comprises those individuals and activities that contribute to this process. For example, crossbred individuals in a multiplier part of a terminal crossbreeding programme would be included to the extent that they contribute information to the breeding of nucleus animals.

We define a breeding programme as a structured, man-driven process in time that starts with a group of individuals X at time 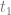and leads to a group of individuals Y at time . The objective of a breeding programme is to transform the genetic characteristics of group X to group Y in a desired direction, and a breeding programme is characterized by the fact that the implemented actions aim at achieving this transformation.

They actually do not elaborate on what it means that a genetic change has direction, but since they want the definition to apply both to farm animal and conservation breeding programmes, the genetic goals could be formulated both in terms of changes in genetic values for traits and in terms of genetic relationships.

Under many circumstances, this is a reasonable proxy also for an economic target: The breeding structures and interventions considered in theoretical breeding programme designs can often be evaluated in terms of their effect on the response to selection, and if the response improves, so will the economic benefit. However, this definition seems a little unnecessary and narrow. If you wanted to, say, add a terminal crossbreeding step to the simulation and evaluate the performance in terms of the total profitability of the crossbreeding programme (that is, something that is outside of the breeding programme in the sense of the above definition), nothing is stopping you, and the idea is not in principle outside of the scope of animal breeding.

Finally, an interesting remark about efficiency

When discussing the possibility of using their concept to communicate breeding programmes to authorities when seeking approval the authors argue that authorities should not take efficiency of the breeding programme into account when they evaluate breeding programmes for approval. They state this point forcefully without explaining their reasoning:

It should be noted, though, that an evaluation of the efficiency of breeding programme is not, and should never be, a precondition for the approval of a breeding programme by the authorities.

This raises the question: why not? There might be both environmental, economical and animal ethical reasons to consider not approving breeding programmes that can be shown to make inefficient use of resources. Maybe such evaluation would be impractical — breeding programme analysis and simulation might have to be put on a firmer scientific grounding and be made more reproducible and transparent before we trust it to make such decisions — but efficiency does seem like an appropriate thing to want in a breeding scheme, also from the perspective of society and the authorities.

I am not advocating any particular new regulation for breeding programmes here, but I wonder where the ”should never” came from. This reads like a comment added to appease a reviewer — the passage is missing from the preprint version.

Literature

Pook, T., Schlather, M., & Simianer, H. (2020a). MoBPS-modular breeding program simulator. G3: Genes, Genomes, Genetics, 10(6), 1915-1918. https://academic.oup.com/g3journal/article/10/6/1915/6026363

Pook, T., Büttgen, L., Ganesan, A., Ha, N. T., & Simianer, H. (2021). MoBPSweb: A web-based framework to simulate and compare breeding programs. G3, 11(2), jkab023. https://academic.oup.com/g3journal/article/11/2/jkab023/6128572

Simianer, H., Büttgen, L., Ganesan, A., Ha, N. T., & Pook, T. (2021). A unifying concept of animal breeding programmes. Journal of Animal Breeding and Genetics, 138 (2), 137-150. https://onlinelibrary.wiley.com/doi/full/10.1111/jbg.12534

Simianer, H. (2021), Harvest Moon: Some personal thoughts on past and future directions in animal breeding research. J Anim Breed Genet, 138: 135-136. https://doi.org/10.1111/jbg.12538

Guest, O., & Martin, A. E. (2020). How computational modeling can force theory building in psychological science. Perspectives on Psychological Science, 1745691620970585. https://journals.sagepub.com/doi/full/10.1177/1745691620970585