In this post, we will look at running two programs that infer population history — understood as changes in linkage disequilibrium over time — from genotype data. The post will chronicle running them on some simulated data; it will be light on theory, and light on methods evaluation.
Linkage disequilibrium, i.e. correlation between alleles at different genetic variants, breaks down over time when alleles are shuffled by recombination. The efficiency of that process depends on the distance between the variants (because variants close to each other on the same chromosome will recombine less often) and the population size (because more individuals means more recombinations). Those relationships mean that the strength of linkage disequilibrium at a particular distance between variants is related to the population size at a particular time. (Roughly, and assuming a lot.) There are several methods that make use of the relationship between effective population size, recombination rate and linkage disequilibrium to estimate population history.
The programs
The two programs we’ll look at are SNeP and GONE. They both first calculate different statistics of pairwise linkage disequilibrium between markers. SNeP groups pairs of markers into groups based on the distance between them, and estimates the effective population size for each group and how many generations ago each group represents. GONE goes further: it uses a formula for the expected linkage disequilibrium from a sequence of effective population sizes and a genetic algorithm to find such a sequence that fits the observed linkage disequilibrium at different distances.
Paper about GONE: Santiago, E., Novo, I., Pardiñas, A. F., Saura, M., Wang, J., & Caballero, A. (2020). Recent demographic history inferred by high-resolution analysis of linkage disequilibrium. Molecular Biology and Evolution, 37(12), 3642-3653.
Paper about SNeP: Barbato, M., Orozco-terWengel, P., Tapio, M., & Bruford, M. W. (2015). SNeP: a tool to estimate trends in recent effective population size trajectories using genome-wide SNP data. Frontiers in genetics, 6, 109.
These methods are suited for estimating recent population history in single closed populations. There are other methods, e.g. the Pairwise Markovian coealescent and methods based on Approximate Bayesian Computation, that try to reach further back in time or deal with connected populations.
(Humorously, barring one capitalisation difference, GONE shares it’s name with an unrelated program related to effective population sizes, GONe … There are not enough linkage disequilibrium puns to go around, I guess.)
Some fake data
First, let us generate some fake data to run the programs on. We will use the Markovian coalescent simulator MaCS inside AlphaSimR. That is, we won’t really make use of any feature of AlphaSimR except that it’s a convenient way to run MaCS.
There is a GitHub repo if you want to follow along.
We simulate a constant population, a population that decreased in size relatively recently, a population that increased in size recently, and a population that decreased in longer ago. The latter should be outside of what these methods can comfortably estimate. Finally, let’s also include a population that has migration from an other (unseen) population. Again, that should be a case these methods struggle with.
Simulated true population histories. Note that the horizontal axis is generations ago, meaning that if you read left to right, it runs backwards in time. This is typical when showing population histories like this, but can be confusing. Also not the different scales on the horizontal axis.
library(AlphaSimR)
library(purrr)
library(tibble)
## Population histories
recent_decrease <- tibble(generations = c(1, 50, 100, 150),
Ne = c(1000, 1500, 2000, 3000))
recent_increase <- tibble(generations = c(1, 50, 100, 150),
Ne = c(3000, 2000, 1500, 1000))
ancient_decrease <- tibble(generations = recent_decrease$generations + 500,
Ne = recent_decrease$Ne)
We can feed these population histories (almost) directly into AlphaSimR’s runMacs2 function. The migration case is a little bit more work because we will to modify the command, but AlphaSimR still helps us. MaCS takes a command line written using the same arguments as the paradigmatic ms program. The runMacs2 function we used above generates the MaCS command line for us; we can ask it to just return the command for us to modify. The split argument tells us that we want two populations that split 100 generations ago.
runMacs2(nInd = 100,
Ne = recent_decrease$Ne[1],
histGen = recent_decrease$generations[-1],
histNe = recent_decrease$Ne[-1],
split = 100,
returnCommand = TRUE)
The resulting command looks like this:
"1e+08 -t 1e-04 -r 4e-05 -I 2 100 100 -eN 0.0125 1.5 -eN 0.025 2 -eN 0.0375 3 -ej 0.025001 2 1"
The first part is the number of basepairs on the chromosome, -t flag is for the population mutation rate ,
-r for the recombination rate (also multiplied by four times the effective population size). The -eN arguments change the population size, and the -ej argument is for splitting and joining populations.
We can check that these numbers make sense: The population mutation rate of 10-4 is the typical per nucleotide mutation rate of 2.5 × 10-8 multiplied by four times the final population size of 1000. The scaled recombination rate of 4 × 10-5 is typical per nucleotide recombination rate of 10-8 multiplied by the same.
The population size changes (-eN arguments) are of the format scaled time followed by a scaling of the final population size. Times are scaled by four times the final population size, again. This means that 0.0125 followed by 1.5 refers to that 4 × 0.0125 × 1000 = 50 generations ago population size was 1.5 times the final population size, namely 1500. And so on.
-I (I assume for ”island” as in the ”island model”) sets up the two populations, each with 100 individuals and a migration rate between them. We modify this by setting it to 200 for the first population (because we want diploid individuals, so we need double the number of chromosomes) and 0 for the other; that is, this ghost population will not be observed, only used to influence the first one by migration. Then we set the third parameter, that AlphaSimR has not used: the migration rate. Again, this is expressed as four times the final population size, so for a migration rate of 0.05 we put 200.
Now we can run all cases to generate samples of 100 individuals.
migration_command <- "1e+08 -t 1e-04 -r 4e-05 -I 2 200 0 200 -eN 0.0125 1.5 -eN 0.025 2 -eN 0.0375 3 -ej 0.025001 2 1"
pops <- list(pop_constant = runMacs2(nInd = 100,
nChr = 5,
histNe = NULL,
histGen = NULL,
Ne = 1000),
pop_recent = runMacs2(nInd = 100,
nChr = 5,
Ne = recent_decrease$Ne[1],
histGen = recent_decrease$generations[-1],
histNe = recent_decrease$Ne[-1]),
pop_increase = runMacs2(nInd = 100,
nChr = 5,
Ne = recent_increase$Ne[1],
histGen = recent_increase$generations[-1],
histNe = recent_increase$Ne[-1]),
pop_ancient = runMacs2(nInd = 100,
nChr = 5,
Ne = ancient_decrease$Ne[1],
histGen = ancient_decrease$generations[-1],
histNe = ancient_decrease$Ne[-1]),
pop_migration = runMacs(nInd = 100,
nChr = 5,
manualCommand = migration_command,
manualGenLen = 1))
Both GONE and SNeP work with text files in Plink ped/map format. Look in the repository if you want to see the not too exciting details of how we extract 10 000 markers and save them to Plink format together with their positions.
Running GONE
GONE source code and binaries are found in their GitHub repository, which we can clone or simply download from the web. As I’m running on Linux, we will use the binaries in the Linux subfolder. Before doing anything else, we will have to set the permissions for each of the binaries stored in the PROGRAMMES directory, with chmod u+x to make them executable.
GONE consists of a set of binaries and a bash script that runs them in order. As the as the script assumes it’s always running from the directory where you put GONE and always writes the output files into the same directory, the easiest way to handle it is to duplicate the entire GONE directory for every run. This also duplicates the INPUT_PARAMETERS_FILE file that one would modify to change settings. Then, invoking GONE with default settings would be as simple as opening a terminal, moving to the working directory and running the script, feeding it the base name of the Plink file:
./script_GONE.sh pop_constant
Thus, we write a prep script like this that copies the entire folder, puts the data into it, and then runs GONE:
#!/bin/bash
## Gone needs all the content of the operating system-specific subfolder to be copied
## into a working directory to run from. Therefore we create the "gone" directory
## and copy in the Linux version of the software from the tools directory.
mkdir gone
cd gone
cp -r ../tools/GONE/Linux/* .
## Loop over all the cases and invoke the GONE runscript. Again, because GONE
## needs the data to be in the same directory, we copy the data files into the
## working directory.
for CASE in pop_constant pop_recent pop_ancient pop_migration pop_increase; do
cp ../simulation/${CASE}.* .
./script_GONE.sh ${CASE}
done
GONE puts its output files (named with the prefixes Output_Ne_, Output_d2_ and OUTPUT_ followed by the base name of the input files) in the same directory. The most interesting is Output_Ne_ which contains the estimates and the all caps OUTPUT_ file that contains logging information about the run.
Estimates look like this:
Ne averages over 40 independent estimates. Generation Geometric_mean 1 1616.29 2 1616.29 3 1616.29 4 1616.29 5 1291.22 6 1221.75 7 1194.16 8 1157.95 ...
And the log looks like this:
TOTAL NUMBER OF SNPs 10000 HARDY-WEINBERG DEVIATION -0.009012 Hardy-Weinberg deviation (sample) -0.003987 Hardy-Weinberg deviation (population) CHROMOSOME 1 NIND(real sample)=100 NSNP=2000 NSNP_calculations=2000 NSNP_+2alleles=0 NSNP_zeroes=0 NSNP_monomorphic=0 NIND_corrected=100.000000 freq_MAF=0.005000 F_dev_HW (sample)=-0.009017 F_dev_HW (pop)=-0.003992 Genetic distances available in map file ...
I will now discuss a couple of issues I ran into. Note, this should not be construed as any kind of criticism of the programs or their authors. Everyone is responsible for their own inability to properly read manuals; I just leave them here in case they are helpful to someone else.
- If you forget to set the permissions of the binaries, the error message will look like this:/
DIVIDE .ped AND .map FILES IN CHROMOSOMES ./script_GONE.sh: line 96: ./PROGRAMMES/MANAGE_CHROMOSOMES2: Permission denied RUNNING ANALYSIS OF CHROMOSOMES ... cp: cannot stat 'chromosome*': No such file or directory bash: ./PROGRAMMES/LD_SNP_REAL3: Permission denied ...
- Whereas Plink allows various different kinds of allele symbols in .ped files, GONE does not like allele codes that don’t look like A, C, G or T. The error message for other symbols looks like this:
DIVIDE .ped AND .map FILES IN CHROMOSOMES RUNNING ANALYSIS OF CHROMOSOMES ... CHROMOSOME ANALYSES took 0 seconds Running GONE Format error in file outfileLD Format error in file outfileLD Format error in file outfileLD Format error in file outfileLD Format error in file outfileLD ...
Running SNeP
SNeP is only available as binaries on its Sourceforge page. Again, I’m using Linux binaries, so I downloaded the Linux binary from there and put it into a tools folder. The binary can be run from any directory, controlling the settings with command line flags. This would run SNeP on one of our simulated datasets, using the Haldane mapping function and correction of linkage disequilibrium values for sample size; these seem to be reasonable defaults:
./SNeP1.1 -ped simulation/pop_constant.ped -out snep/pop_constant -samplesize 2 -haldane
Thus, we write a run script like this:
#!/bin/bash
## As opposed to GONE, SNeP comes as one binary that can run from any directory. We still create
## a working directory to keep the output files in.
mkdir snep
## We loop over all cases, reading the data from the "simulation" directory,
## and directing the output to the "snep" directory. The settings are to
## correct r-squared for sample size using the factor 2, and to use the Haldane
## mapping function. We direct the output to a text file for logging purposes.
for CASE in pop_constant pop_recent pop_ancient pop_migration pop_increase; do
./tools/snep/SNeP1.1 \
-ped simulation/${CASE}.ped \
-out snep/${CASE} \
-samplesize 2 \
-haldane > snep/${CASE}_out.txt
done
SNeP creates two ouptut files with the given prefix, one with the extension .NeAll with the estimates a log file with the suffix SNeP.log file. Above, we also save the standard output to another log file.
Estimates look like this:
GenAgo Ne dist r2 r2SD items 13 593 3750544 0.0165248 0.0241242 37756 15 628 3272690 0.017411 0.0256172 34416 18 661 2843495 0.0184924 0.0281098 30785 20 681 2460406 0.0200596 0.0310288 27618 24 721 2117017 0.0214468 0.0313662 24898 ...
Issues I ran into:
- There are two versions of SNeP on Sourceforge, version 1.1 and version 11.1. According to the readme, SNeP requires ”GCC 4.8.2 or newer”, which I guess is a way to say that it needs a recent enough version of GLIBC, the runtime library that includes the C++ standard library. SNeP 1.11 appears to depend on GLIBC 2.29, and because I have 2.27, I had to use SNeP version 1.1 instead. It might be possible that it doesn’t require the new version of glibc, and that one could build from source on my system — but the source is not available, so who knows; this is a problem with distributing software as binaries only.
- You cannot specify just a file name for your output. It needs to be a directory followed by a file name; that is, ”snep_constant” is not okay, but ”./snep_constant” is. The error looks like this:
/tools/snep/SNeP1.1 -ped constant.ped -out snep_constant ************************************* * SNeP * * v1.1 * * barbatom@cardiff.ac.uk * ************************************* Sat Dec 25 13:09:38 2021 The -out path provided gives an error, aborting.
The moment you’ve been waiting for
Let’s read the results and look at the estimates!
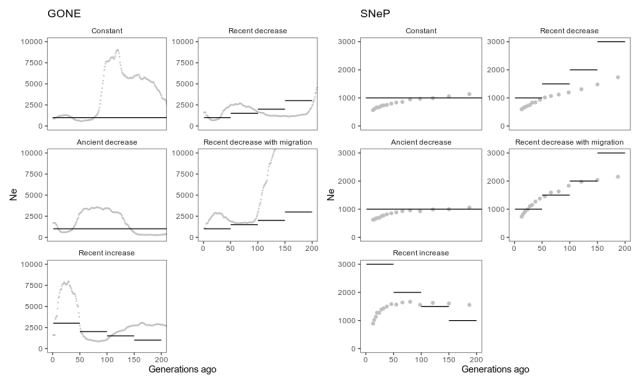
Estimates from GONE, with default settings, and SNeP, with reasonable setting used in the SNeP paper, applied to simulated data from different scenarios. Grey dots are estimates, and black lines the true simulated population history. The estimates go on for a while, but as per the GONE paper’s recommendations, we should not pay attention to estimates further back in time where these methods are not accurate. That is, we should probably concentrate on the first 100 generations or so.
Again, this isn’t a systematic methods evaluation, so this shouldn’t be taken as a criticism of the programs or methods. But we can note that in these circumstances, the estimates capture some features of the simulated population histories but gets other features quite wrong. GONE estimates a recent decrease in the scenario with a recent decrease, but not the further decreases before, and a recent increase when there was a recent increase, but overestimates its size by a few thousand. In the migration scenario, GONE shows the kind of artefact the authors tell us to expect, namely a drastic population size drop. Unexpectedly, though, it estimates a similar drastic drop in the scenario with constant population size. SNeP captures the recent decrease, but underestimates its size. In fact, SNeP estimates a similar shape in all scenarios, both for increased, decreased and constant populations.
The plotting code looks something like this (see GitHub for the details): we create the file names, read all the output files into the same data frame with map_dfr, label them by what case they belong to by joining with the data frame of labels (with inner_join from dplyr) and make a plot with ggplot2. The true_descriptions data frame contains the true population histories used to simulate the data.
library(ggplot2)
library(readr)
cases <- tibble(case = c("pop_constant",
"pop_recent",
"pop_ancient",
"pop_migration",
"pop_increase"),
description = c("Constant",
"Recent decrease",
"Ancient decrease",
"Recent decrease with migration",
"Recent increase"))
snep_file_names <- paste("snep/", cases$case, ".NeAll", sep = "")
names(snep_file_names) <- cases$case
snep <- map_dfr(snep_file_names, read_tsv, .id = "case")
snep_descriptions <- inner_join(snep, cases)
snep_descriptions$description <- factor(snep_descriptions$description,
levels = cases$description)
## Make both a plot of the entire range of estimates, and a plot of the
## first 200 generations, which is the region where estimates are expected
## to be of higher quality
plot_snep_unconstrained <- ggplot() +
geom_point(aes(x = GenAgo, y = Ne),
data = snep_descriptions,
colour = "grey") +
facet_wrap(~ description,
scale = "free_y",
ncol = 2) +
geom_segment(aes(x = start,
y = Ne,
xend = end,
yend = Ne),
data = true_descriptions) +
theme_bw() +
theme(panel.grid = element_blank(),
strip.background = element_blank()) +
xlab("Generations ago")
plot_snep <- plot_snep_unconstrained +
coord_cartesian(xlim = c(0, 200), ylim = c(0, 3000))
När kartan inte stämmer med terrängen gäller terrängen
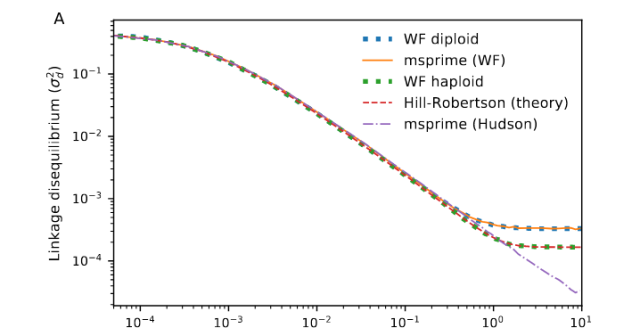
When the results of a method don’t agree with the parameters of simulated data, the problem can either lie with the method or with the simulated data. And in this case, coalescent simulation is known to have problems with linkage disequilibrium. Here is a figure (Fig A, of appendix 2) of Nelson et al. (2020) who study the problems with coalescent simulations over long regions (such as the ones we simulated here).
The problem occurs for variants that are far apart (e.g. at around 100 = 1 expected recombinations between loci), where there should still be linkage disequilibrium, whereas the coalescent simulator (in this figure, ”msprime (Hudson)”) gives too low linkage disequilibrium. When we try to estimate effective population size late in population history, the methods rely on linkage equilibrium between markers far apart, and if they have too low linkage disequilibrium, the estimated population size should be too large. This does not appear to be what is going on here, but there might be more subtle problems with the simulated linkage disequilibrium that fools these methods; we could try something like Nelson et al.’s hybrid method or a forward simulation instead.
Literature
Barbato, M., Orozco-terWengel, P., Tapio, M., & Bruford, M. W. (2015). SNeP: a tool to estimate trends in recent effective population size trajectories using genome-wide SNP data. Frontiers in genetics, 6, 109.
Nelson, D., Kelleher, J., Ragsdale, A. P., Moreau, C., McVean, G., & Gravel, S. (2020). Accounting for long-range correlations in genome-wide simulations of large cohorts. PLoS genetics, 16(5), e1008619.
Santiago, E., Novo, I., Pardiñas, A. F., Saura, M., Wang, J., & Caballero, A. (2020). Recent demographic history inferred by high-resolution analysis of linkage disequilibrium. Molecular Biology and Evolution, 37(12), 3642-3653.